О теории бильярда и не только

Обсуждение в комментариях к «золотым зонам» Калюжного напомнило мне одну старую историю. В начале 2000-ых, будучи ещё не знаком с трудами по теории бильярда (работами Кориолиса, Шепарда, Дэйва и пр.) я озадачился проверить преимущество правила сыгрывания битка накатом с резкой в полшара. Другими словами, вычислить резку, при которой угол проката битка максимален.
Я исходил из энергетических соображений. Энергия катящегося битка складывается из энергии его поступательного движения Еv = mV^2/2 и энергии его вращения Еw = Jw^2/2, где m-масса шара, V- скорость центра шара, J – момент инерции шара, w – скорость вращения шара. Учитывая, что при качении (накате) w = V/R, где R – это радиус шара, а также, что момент инерции шара J=2mR^2/5, не трудно увидеть, что при накате энергия вращения будет Еw =mV^2/5, то есть составляет 2/5 от энергии поступательного движения шара Еv, не зависимо от величины скорости этого движения. Еw = 0,4 Еv
Дальше, нарисовав несложную диаграмму, я рассуждал так : При соударении с прицельным шаром энергия поступательного движения битка перераспределяется между битком и ПШ, которые отскакивают друг от друга под прямым углом – биток по касательной к точке соударения, а ПШ по нормали.
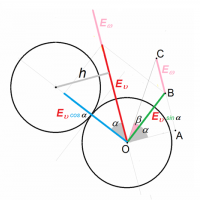
Угол резки α определяется равенством sin α = h/(2R), где h – величина резки (катет в прямоугольном треугольнике с гипотенузой 2R). Соответственно энергия отскока битка равна Еv sin α . Дальше, чтобы найти угол β отклонения битка от действия вращения, рассматривая треугольники ОАВ и ОАС имеем :
tg(α+β) = AC/ОА = (АВ+ВС)/ОА = (Еv sin α sin α + Еw)/ (Еv sin α cos α).
Подставляя выражение для Еw и сокращая в числителе и знаменателе дроби Еv, получаем: tg(α+β) = (sin α sin α + 2/5)/(sin α cos α). (*)
Учитывая, что тангенс функция монотонно возрастающая, задача нахождения максимума аргумента тангенса сводится к нахождению максимума самого тангенса. То есть приравнивая к нулю производную правой части уравнения и находя значение α. Но лучше искать не α , а долю резки Х (репер) выраженную в отношении величины резки к радиусу x = h/R = 2 sin α .
Подставляя эту замену в правую часть уравнения выше, получим уравнение для нахождения оптимальной резки :
(0.25 x ^2 + 0.4)/(0.5 x (1 – 0.25 x ^2)^0.5) ` = 0
Что, после вычисления производной по x и решения алгебраического уравнения, даёт значение оптимального репера Хопт = 2√2/3 =0,94281. То есть резка почти равна радиусу (в просторечии полшара). Точно такой же результат получен Шепардом и Дэйвом.

Казалось бы здорово. Хорошо известное практическое правило проверено расчётом. Но нет ! Абсолютно правильный результат получен путём ошибочных построений ! Дело в том, что энергия не векторная величина, а скалярная, и раскладывается по касательной и нормали для битка и прицельного шара пропорционально не синусу и косинусу угла резки, а пропорционально их квадратам (как известно sin^2 α + cos^2 α =1). Соответственно синий и зелёный отрезки на диаграмме должны быть короче, что дало бы совсем другой, несколько больший угол отклонения β.
Почему же результат оказался верный при неверных построениях ? Ответ заключается в том, что в действительности не вся энергия вращения (наката) битка расходуется на отклонение его траектории при отскоке от ПШ. Некоторая часть остаётся, и это выражается в наклоне оси вращения(качения) битка при его прямолинейном качении после криволинейного участка скольжения. Правильное уравнение (*), равносильное уравнению (38) Dr.Dave http://billiards.colostate.edu/technical_proofs/new/TP_A-4.pdf , получено совершенно случайно. :-^)

К чему это я всё ? А к тому, что даже верный результат можно получить при небрежном/невнимательном отношении к исследуемой задаче и неверном применении знаний в области физики, геометрии, алгебры. Получить же заведомо неверный результат намного более вероятно. Как это произошло у Калюжного. Поэтому, прежде чем изобретать велосипед, друзья, не мешает изучить, какие ЗНАНИЯ по волнующему вас вопросу накопило человечество. :-^)


Зри в корень ! (с) Козьма Прутков